Применение алгебры логики в информатике (понятия, формулы)

метки: Логический, Данные, Условие, Высказывание, Алгебра, Переменный, Стоимость, Материал

Логика в информатике – это направления исследований и отрасли знания, где логика применяется в информатике и искусственном интеллекте.

Современный прогресс, развитие науки и техники, достижения в компьютерных технологиях базируются на знаниях основ алгебры логики. Роль алгебры логики в информатике очень весома, так как принципы работы любого компьютера, его схем и функциональных блоков основаны на ее законах.

Математическая логика нашла широкое применение в языках программирования. Все языки программирования включают в себя базовые логические операции и некоторые логические функции: IMP, EQL, и так далее.

В данной работе будут рассмотрены основные аспекты алгебры логики, понятия, виды логических операций и таблиц истинности, логические формулы, а также законы алгебры логики. Заключительная часть посвящена использованию алгебры логики в компьютерных науках.

В практической части будет построена компьютерная модель решения задачи в среде MS Excel.

1. Теоретическая часть

1.1 Основные понятия и определения

Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

При этом под высказыванием (суждением) понимают повествовательное предложение, относительно которого можно сказать, истинно или ложно.

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Её создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Долгое время алгебра логики была известна достаточно узкому классу специалистов. Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 Клод Шеннон (1916 — 2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования релейно-контактных и электронно-ламповых схем.

Алгебра логики явилась математической основой теории электрических и электронных переключателей схем, используемых в ЭВМ. В компьютерных науках её предпочитают называть не алгеброй логики, а Булевой алгеброй — по имени её создателя.

Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например, {0,1}).

Компьютерная лингвистика

... и многие другие. Данная работа посвящена построению оптимального компьютерного интерфейса средствами компьютерной лингвистики при проведении лингвистических исследований. 1. Место и роль компьютерной лингвистики в лингвистических исследованиях В ... их тематическое содержание, а поисковые образы запросов – в виде логических конструкций, в которых ключевые слова и словосочетания соединялись друг с ...

Иногда вместо термина «алгебра логики» употребляют термин «двузначная логика».

В компьютерах булевы переменные представляются (кодируются) битами (разрядами двоичной системы счисления), где 1 означает истину, а 0 — ложь. Манипуляции высказываниями и их комбинациями используются для получения некоего единственного результата, который можно использовать, например, для выбора той или иной последовательности действий. Поскольку логические переменные кодируются по тем же принципам, что и числа, символы и прочая информация, то можно комбинировать операции логики с

операциями арифметики для реализации различных алгоритмов.

Таким образом, алгебра логики — это область математики. Она оперирует величинами, которые могут принимать два значения (булевых значения).

Эти два значения могут быть обозначены как угодно, лишь бы по-разному. Самые распространенные варианты:

0, 1 F, T false, true ложь, истина Л, И

При применении булевой алгебры в вычислительной технике, булевы значения — это 0 и 1. Они представляют собой состояние ячейки памяти объёмом в 1 бит или наличие/отсутствие напряжения в электрической схеме. Алгебра логики позволяет строить сложные электронные узлы, элементы которых работают согласно этой математической теории. При применении булевой алгебры в логических построениях в математике, булевы значения — это «ложь» и «истина». Они определяют истинность или ложность некоторого высказывания. Под высказываниями понимаются математические формулы. При применении булевой алгебры в повседневных рассуждениях, булевы значения — это также «ложь» и «истина». Они представляют собой оценку истинности или ложности некоторого высказывания. Под высказываниями понимаются фразы, которые удовлетворяют строго определенному списку свойств.

Логическое выражение — это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные буквами латинского алфавита.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

1.2. Основные логические операции и элементы

Операция отрицания.

Операция логического отрицания осуществляется над одним высказыванием. Выполнить операцию логического отрицания (обозначается ) — значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Например, если А = «Луна — спутник Земли», то = «неверно, что Луна — спутник Земли», что ложно. Истинность высказывания определяется таблицей:

Отрицание
А
1	0
0	1

Отсюда следует, что отрицание высказывания истинно тогда и только тогда, когда высказывание А ложно.

Операция конъюнкции.

Конъюнкция (логическое умножение) соответствует союзу «и» в русском языке. Конъюнкция двух высказываний истинна тогда и только тогда, когда оба составляющих высказывания истинны.

Например, пусть есть два истинных высказывания А = «Земля круглая» и В = «Луна – спутник Земли», тогда их конъюнкцией будет также истинное высказывание «Земля круглая и Луна — спутник Земли» (А=1, В=1; 1·1=1).

В случае если хотя бы одно из высказываний ложно, например В = «Марс — спутник Земли», их конъюнкция «Земля круглая и Марс — спутник Земли» также будет ложным высказыванием (А=1, В=0; 1·0=0).

Истинность конъюнкции определяется таблицей:

Конъюнкция
А	В	А ∙ В
0	0	0
0	1	0
1	0	0
1	1	1

Операция дизъюнкции.

Дизъюнкция (логическое сложение) соответствует союзу «или» в русском языке. Например, высказывания A = «Декабрь — зимний месяц», В = «В январе сильный мороз». Определим высказывание A + B как «Декабрь — зимний месяц или в январе сильный мороз» (А=1; В=1 или В=0; 1+1=1 или 1+0=1).

Дизъюнкция истинна, если хотя бы одно из высказываний истинно. Установить истинность логической суммы можно с помощью следующей таблицы:

Дизъюнкция
А	В	А + В
0	0	0
0	1	1
1	0	1
1	1	1

То есть дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны.

Эквиваленция высказываний А, В — это высказывание, обозначаемое А↔В и определяемое следующей таблицей. Эквиваленция истинна тогда и только тогда, когда образующие ее высказывания А, В имеют одинаковые значения.

Эквиваленция
А	В	А ↔ В
0	0	1
0	1	0
1	0	0
1	1	1

Импликация.

Импликации соответствуют конструкции «Если…, то…» («Из… следует…»).

Импликация высказываний А и В обозначается как А→В.

Импликация А→В ложна тогда и только тогда, когда А — истина, В — ложь. Допустим А = «Цены высоки» и В = «Товаров продано мало». Тогда импликация А→В является истинным высказыванием. Элементы высказывания, образующего импликацию, имеют специальные названия: А— посылка (гипотеза, антецедент), В— заключение (вывод, консеквент).

Ее истинность определяется следующей таблицей:

Импликация
А	В	А → В
0	0	1
0	1	1
1	0	0
1	1	1

1.3. Логические формулы. Законы алгебры логики

Предметом алгебры логики являются высказывания, операции над ними, а также логические функции. При этом для обозначения высказываний используются буквы.

Логическая переменная — переменная, значением которой может быть любое высказывание. Логические переменные обозначаются латинскими буквами, иногда снабжёнными индексами, как обычные алгебраические переменные.

Понятие логической формулы является формализацией понятия сложного высказывания.

Логической формулой является: 1) любая логическая переменная, а также каждая из двух логических констант – 0 (ложь) и 1 (истина).

2) Если А и В – формулы, то В и А*В – тоже формулы, где знак «*» означает любую из логических бинарных операций. Формулой является, например, выражение: (x&y) → z. Каждой формуле при заданных значениях входящих в неё переменных приписывается одно из двух значений – 0 или 1. Формулы А и В, зависящие от одного и того же набора переменных , называют равносильными или эквивалентными, если на любом наборе значений переменных они имеют одинаковые значения. Для обозначения равносильности формул используется знак равенства, например А=В.

Любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введённые операции &, ∨ и отрицание.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Определение логической формулы:

1. Всякая логическая переменная и символы «истина» (1) и «ложь (0) — формулы.

2. Если А и В — формулы, то , АВ, АvВ, А→B, А↔В — формулы.

3. Никаких других формул в алгебре логики нет.

Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел называют законами:

1) Законы коммутативности

х & y = y & x, x ∨ y = y ∨ x;

2) Законы ассоциативности

(x & y) & z = x & (y & z), (x ∨ y) ∨ z = x ∨ (y ∨ z);

3)Законы поглощения (нуля и единицы)

х ∨ 0 = x, x & 1= x;

4) Законы дистрибутивности

х & (y ∨ z) = (x & y) ∨ (x & z), x ∨ (y & z) = (x ∨ y) & (x ∨z);

5) Закон противоречия

х ∨ = 0;

6) Закон исключённого третьего

х ∨ = 1;

7) Закон идемпотентности

х & x = x, x ∨ x = x;

8) Закон двойного отрицания;

=

9) Законы де Моргана

−−−− −−−−

= , = ,

9) Законы поглощения

х ∨ (x & y) = x, x & (x ∨ y) = x.

Любой из этих законов может быть доказан с помощью таблиц истинности.

Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. Таблица истинности от n переменных состоит из 2n +1 строк и n +1 столбцов.

Пример. Составить таблицу истинности для функции f трех переменных x1, x2, x3, которая равна единице в случае, если только одна из входных переменных равна 1.

Таблица истинности для функции f

Входные переменные			Выходная переменная
х1	х2	х3	f
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	0

Переменная х в функции f называется фиктивной (несущественной), если значение переменной х не влияет на значение булевой функции. Фиктивные переменные могут быть удалены или введены в набор переменных функций. Количество булевых функций определяется числом n переменных

1.4. Применение алгебры логики в информатике

После изготовления первого компьютера стало ясно, что при его производстве возможно использование только цифровых технологий – ограничение сигналов связи единицей и нулём для большей надёжности и простоты архитектуры компьютера. Благодаря своей бинарной природе, математическая логика получила широкое распространение в вычислительной технике и информатике. Были созданы электронные эквиваленты логических функций, что позволило применять методы упрощения булевых выражений к упрощению электрической схемы. Кроме того, благодаря возможности нахождения исходной функции по таблице позволило сократить время поиска необходимой логической схемы.

В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер.

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: «1» и «0».

Из этого следует два вывода:

1) одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;

2) на этапе конструирования аппаратных средств алгебра логики позволяет

значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации.

В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например: Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И — НЕ, ИЛИ — НЕ и другие (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния – «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению «истина» (1), а низкий — значению «ложь»(0).

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нём реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности.

Булевы алгебры находят применение главным образом в теории множеств, в математической логике, в теории вероятностей и в функциональном анализе.

Итак, алгебра логики применяется: 1) для упрощения сложных логических формул и доказательств тождеств; 2) при решении логических задач; 3) в контактных схемах; 4) при доказательствах теорем; 5) в базах данных при составлении запросов.

1.5. Реализация функций алгебры логики, электронные схемы.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.

Схема И реализует конъюнкцию двух и более логических значений.

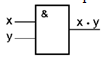
Схема ИЛИ

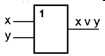
Схема НЕ (инвертор) реализует операцию отрицания.

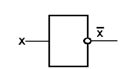
Схема И—НЕ

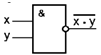
Схема ИЛИ—НЕ

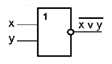
Триггер — электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. Данные схемы осуществляют запоминание информации и остаются в заданном состоянии после прекращения действия переключающих сигналов. Условное обозначение триггера представлено на рис.1.

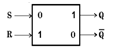
Рис.1. Условное обозначение RS-триггера

Он имеет два симметричных входа S и R и два симметричных выхода Q и , причем выходной сигнал Q является логическим отрицанием сигнала . На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( ).

Наличие импульса на входе будем считать единицей, а его отсутствие — нулём. На Рис.2 показана реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.

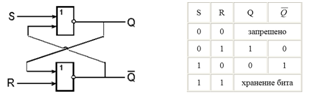
Рис.2. Реализация триггера с помощью вентилей ИЛИ-НЕ и его таблица истинности

По способу организации логических связей, определяющие особенности функционирования, различают триггеры RS, T, D, JK. Из них JK триггер называется универсальным, так как из него можно получить все остальные виды триггеров.

Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8= 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.

Сумматор — электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.

Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, который будет здесь рассмотрен. Условное обозначение одноразрядного сумматора представлено на Рис.3.

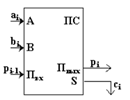
При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами: 1.цифра ai первого слагаемого; 2. цифра bi второго слагаемого; 3. перенос pi –1 из младшего разряда. В результате сложения получаются две цифры: 1. цифра ci для суммы; 2. перенос pi из данного разряда в старший.

Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:

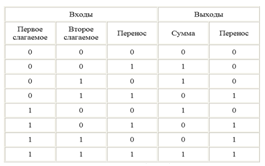
Переключательная схема

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.

Найдем функции проводимости F некоторых переключательных схем:

а)

Схема не содержит переключателей и проводит ток всегда, следовательно F =1;

б)

Схема содержит один постоянно разомкнутый контакт, следовательно, F = 0;

в)

Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(х) = х;

г)

Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(х) = х;

д) Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(х) = х∙y

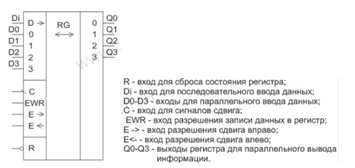
Регистры – это узлы ЭВМ, служащие для хранения информации в виде машинных слов или его частей, а так же для выполнения над словами некоторых логических преобразований. Они представляют собой цифровые автоматы Мили, выполненные на триггерах.

Регистры способны выполнять следующие операции:

• установка регистра в состояние 0 или 1 (на всех выходах);
• прием и хранение в регистре n разрядного слова;
• сдвиг хранимого в регистре двоичного кода слова вправо или влево на заданное значение разрядов;
• преобразование кода хранимого слова в последовательный, и наоборот, при приеме или при выдачи двоичных данных;
• поразрядные логические операции.

Ниже показано условно графическое обозначение универсального регистра и назначение его выводов:

2. Практическая часть

2.1. Постановка задачи

Негосударственное образовательное учреждение НОУ «Креатив» организует творческие курсы для населения города. Проведение тео­ретических и практических занятий включает почасовую оплату пре­подавателя и накладные расходы. Дополнительно слушатели также оплачивают стоимость раздаточного материала для проведения прак­тических занятий. Данные для выполнения расчетов представлены на рис. 1 и 2.

Для решения задачи необходимо следующее.

1. Построить таблицы по данным, приведенным на рис. 1 и 2.

2. Рассчитать общую стоимость каждого вида творческих курсов без учета раздаточного материала (рис. 1).

3. Рассчитать стоимость раздаточного материала для проведения практических занятий по каждому курсу на одного человека (рис. 2).

4. Организовать межтабличные связи с использованием функций ВПР или ПРОСМОТР для автоматического формирования дохода от проведенных курсов.

5. Сформировать и заполнить таблицу с данными по расчету дохода от проведенных курсов с учетом количества слушателей, стоимости курсов и стоимости раздаточного материала по каждому виду кур­сов и по всем курсам в целом (рис. 3).

6. Результаты расчетов доходов по каждому виду проведенных курсов представить в графическом виде.

Стоимость курсов на одного человека без учета раздаточного материала

№ п/п	Название курса	Теоретический курс, руб.	Практические занятия, руб.	Стоимость курса, руб.
1		567	3564
2	«Роспись по ткани»	438	3328
3	«Мыловарение»	522	1145
4	«Гончарное дело»	865	3657
5	«Ткачество»	741	2987
6	«Мозаика, витраж»	659	2564

Рис. 1. Данные о стоимости курсов

Стоимость раздаточного материала для проведения практических занятий по каждому курсу на одного человека

№ п/п	Название курса	Количество практических занятий, час.	Стоимость раздаточного материала на 1 чел., руб	Стоимость раздаточного материала на все практические занятия по курсу на 1 чел., руб.
1		16	74
2	«Роспись по ткани»	12	66
3	«Мыловарение»	8	85
4	«Гончарное дело»	16	54
5	«Ткачество»	10	65
6	«Мозаика, витраж»	12	61

Рис. 2. Данные о стоимости раздаточного материала для проведения практических занятий

Доход НОУ «Креатив» от проведенных курсов в текущем месяце.

№ п/п	Название курса	Количество слушателей, чел.	Стоимость курса на 1 чел., руб.	Стоимость раздаточного материала на 1 чел., руб.	Доход от проведенных курсов, руб.
1		59
2	«Роспись по ткани»	48
3	«Мыловарение»	97
4	«Гончарное дело»	54
5	«Ткачество»	49
6	«Мозаика, витраж»	58
Итого общий доход от курсов, руб.

Рис. 3. Расчет дохода от проведенных курсов

2.1.1.Цель решения задачи

Целью решения данной задачи является расчет стоимости каждого вида творческих курсов, а также автоматизация процесса расчета доходов от проведенных курсов.

2.1.2 Условие задачи

Входной оперативной информацией служит документ «Ведомость стоимости раздаточного материала на 1 человека», содержащий следующие реквизиты: наименование курса, количество практических занятий, стоимость раздаточного материала на 1 человека, стоимость раздаточного материала на все практические занятия по курсу на 1 человека. На основании этого документа создается следующая экранная форма:

Ведомость стоимости раздаточного материала на 1 человека

Наименование курса	Количество практических занятий, час.	Стоимость раздаточного материала на 1 чел., руб.	Стоимость раздаточного материала на все практические занятия по курсу на 1 чел., руб.
m	Km	Rm	Dm

Условно-постоянной информацией служит справочник: «Справочник стоимости курсов», содержащий следующие реквизиты: наименование курса, стоимость теоретических и практических занятий, стоимость курса. На основании справочника создается его экранная форма:

Справочник стоимости курсов на 1 человека (без учета раздаточного материала)

Наименование курса	Теоретический курс, руб.	Практические занятия, руб.		Стоимость курса, руб.
m	Tm		Pm	Sm

Результирующей информацией будет служить документ «Доход от проведенных курсов». Экранная форма выходного документа:

«Ведомость о доходах от проведенных курсов»

Наименование курса	Количество слушателей	Стоимость курса, руб.	Стоимость раздаточного материала на все практические занятия по курсу на 1 чел., руб.	Доход от проведенных курсов, руб.
m	Lm	Sm	Dm	Cm
Общий итог				С

2.2 Компьютерную модель решения задачи смотрите в файле

Заключение

Алгебра логики — важнейший раздел современной информатики.

Итак, математическая логика возникла задолго до появления компьютеров и возникла она в результате необходимости в строгом формальном языке. Были построены функции — удобное средство для построения сложных утверждений и проверки их истинности. Оказалось, что такие функции обладают аналогичными свойствами с алгебраическими операторами. Это дало возможность упрощать исходные выражения. Особое свойство логических выражений — возможность их нахождения по значениям. Это получило широкое распространение в цифровой электронике, где используются логические элементы, и программировании.

Алгебра логики применяется: 1) для упрощения сложных логических формул и доказательств тождеств; 2) при решении логических задач; 3) в контактных схемах; 4) при доказательствах теорем; 5) в базах данных при составлении запросов.

В практической части курсовой работы была решена задача по расчету «Дохода от проведенных курсов», построена гистограмма на основе результата составленного документа.

Список использованной литературы

[Электронный ресурс]//URL: https://litfac.ru/kursovaya/logicheskie-usloviya-vyibora-dannyih/

1. Агальцов В.П., Титов В.М. Информатика для экономистов: учебник. – М.: Форум: ИНФРА-М, 2006.

2. Информатика в экономике: учебное пособие / под ред. Б.Е. Одинцова, А.Н. Романова. – М.: Вузовский учебник, 2008.

3. Попов А.М. Информатика и математика: учеб. пособие. – М.: ЮНИТИ-ДАНА, 2012.

4. Бекман И.Н. Компьютеры в информатике. Логические основы компьютеров. — http://profbeckman.narod.ru/EVM.files/Komp6.pdf

---

не сложно

Важно! Все представленные Курсовые работы для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

---

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

---

Если Курсовая работа, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, об этом нам.

---