«»Волшебник» из Багдада»

метки: Хорезми, Творчество, Уравнение, Число, Слово, История, Джафар, Шесть

« Я составил краткую книгу об исчислении

алгебры и алмукабалы, заключающую в себе

простые и сложные вопросы арифметики, ибо это необходимо людям».

Аль-Хорезми

Аль-Хорезми Мухаммед бен-Муса (783-850)

«Волшебник» из Багдада

В рамках внеурочного курса по математике «Удивительный мир чисел» мы познакомились с выдающимся арабским математиком и астроном Абу Абдалах Мухаммед Бен Мусса аль – Хорезми. Что же это за математик из древности, незримо присутствующий на уроках математики много веков спустя?

Ответ на этот вопрос мы и попыталась найти в данной работе.

«Волшебник» из Багдада

Багдад был основан в 60-х гг. VIII в. халифом ал-Мамун-ром из династии Аббасидов, правившим с 754 по 775 год. Новая столица государства, занимавшего в то время огромную территорию, быстро стала важным центром торговли, науки и культуры. Управлять огромным государством было нелегко. Правители халифата поняли, что их экономические и военные планы нельзя воплотить в жизнь, если не будут освоены те знания, которыми владели покоренные народы. Поэтому повелители всемерно содействовали развитию науки. В Багдаде возникла крупная научная школа, которая привлекала к себе выдающихся ученых из разных стран. Была создана библиотека, пополнявшаяся ценными научными трудами. Они стали приглашать в Багдад виднейших ученых из покоренных стран.

До 813 года ал-Мамун был наместником восточных провинций и жил в Мерве. Не исключено, что здесь он и встретился с ал-Хорезми, а впоследствии пригласил его в Багдад. В одном из своих сочинений ал-Хорезми с похвалой отозвался об ал-Мамуне. Он отмечал его «любовь к науке и стремление приближать к себе ученых, простирая над ними крыло своего покровительства и помогая им в разъяснении того, что для них неясно, и в облегчении того, что для них затруднительно».

Аль-Хорезми — великий математик, астроном и географ, основатель классической алгебры. В исторических источниках нет упоминания о конкретном месте рождения Аль Хорезми, но некоторые косвенные соображения позволяют допустить, что он происходил из древней Хивы.

Полное имя ал-Хорезми — Абу Абдаллах (или Абу Джафар) Мухаммед ибн Муса ал-Хорезми. Что же скрывается под этим именем?

Арабы имеют привычку прятать в имени человека целую биографию:

Применение алгебры логики в информатике (понятия, формулы)

... электронные узлы, элементы которых работают согласно этой математической теории. При применении булевой алгебры в логических построениях в математике, булевы значения - это «ложь» и «истина». Они ... некоего единственного результата, который можно использовать, например, для выбора той или иной последовательности действий. Поскольку логические переменные кодируются по тем же принципам, что и ...

Абу Абдуллах (или Абу Джафар) Мухаммед ибн Муса Аль-Хорезми -Абу — означает «Отец кого-то». Другими словами, Абу Абдуллах (или Абу Джафар) означает, что у него было как минимум два сына: Абдулла и Джафар. Мухаммед ибн Муса Аль-Хорезми — имя ученого – Мухаммед, ибн с арабского означает «Сын». Значит, отца ученого звали Муса.

Более того, теперь мы можем сразу сказать, откуда ученый был родом.

Слова «Аль-где-то» указывают, что Мухаммед Аль-Хорезми был родом из Хорезма. Ныне Хорезм — это город в Узбекистане.

Оказывается, что Узбекистан и есть то звено в «исторической цепочке», откуда к нам пришло наше современное математическое знание с ее строгой логикой.

В некоторых исторических источниках Аль-Хорезми назван «ал-маджуси», т. е. маг. Из этого заключают, что его предки были магами — жрецами зороастрийской религии, распространенной на территории Средней Азии. Это даёт повод считать, что одним из источников знаний Мухаммеда Аль-Хорезми была наука доисламской Средней Азии, хранителями которой были маги.

Биографических сведений об Аль-Хорезми история почти не сохранила. До нас не дошли даже точные даты его рождения и смерти. Известно лишь, что он родился в конце восьмого века, а умер во второй половине девятого, точнее после 847 г. Сейчас условно принято считать годом его рождения 783, а годом смерти 850 год.

Известно, что он возглавлял в Багдаде библиотеку Дома мудрости, своего рода Багдадской академии, при халифе ал-Мамуне. А при другом халифе ал-Васике, преемнике ал-Мамуна, он возглавлял экспедицию к хазарам.

Наиболее поздняя дата, связанная с именем Аль-Хорезми, — 847 год. В этом году умер халиф ал-Васик, и ал-Хорезми упоминается среди лиц, присутствовавших при его кончине.

Таким образом, мы видим, что фактов из жизни великого среднеазиатского ученого сохранилось очень мало. Поэтому историки науки основываются главным образом на исследовании его трудов.

Математические трактаты

Mafatih al-‘Ulum

• местные знания — юриспруденция, схоластическая философия, грамматика, секретарские обязанности, просодия и поэтическое искусство, история;

• иностранные знания — философия, логика, медицина, арифметика, геометрия, астрономия, музыка, механика, алхимия.

Algoritmi de numero Indorum

Kitab al-jabr wa l-muqabala

Оба математических трактата служили долгое время основными учебниками по математики. Остановимся более подробно на них.

«Книга об индийском счете»

В «Книге об индийском счёте» Мухаммед ибн Мусса подробно описал правила, по которым надо выполнять арифметические действия. Некоторые из них были похожи на применяемые сейчас. Например, сложение и вычитание столбиком.

А вот правила умножения и деления были иными. Для умножения чисел Аль-Хорезми предлагал «метод решетки», в некотором роде проще, чем применяемый в школе. Пусть надо умножить 347 на 29. Начертим таблицы:

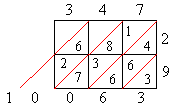
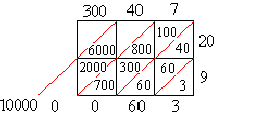Таблица 1. Умножение Таблица 2. Умножение по разрядам

Художественный образ и научное понятие: сравнительно-эпистемологический анализ

... поэтому мы упомянули об эстетической, "ничем не заменимой функции искусства". В связи с этим о художественном образе можно говорить как о средстве достижения вышеозначенной цели; о тех ... научился мыслить отвлеченно и анализировать, т.е. когда зародились разные способы отражения реальности. Может показаться, что оформившийся художественный образ есть полная противоположность научного понятия, но на ...

Над Таблицей 1 надпишем 347 слева направо, а справа от неё – число 29 сверху вниз. В каждую клеточку запишем произведение цифр, стоящих над этой клеточкой и справа от неё. При этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней.

А теперь будем складывать числа в каждой косой полосе, выполняя эту операцию справа налево. Если сумма окажется меньше 10, то её пишут под нижней цифрой полосы. Если же сумма окажется больше 10, то пишут только цифру единиц суммы, а цифру десятков прибавляют к следующей сумме. В результате получаем нужное произведение: 10063.

Этот способ умножения был очень распространен раньше на Востоке и в Италии. Разбирая его смысл, видим, что в первой косой полосе стоят единицы, во второй – десятки, в третьей – сотни и т.д.

Таким образом, произведение 347 на 29 вычисляется(Таблица 2):

347

• 29 = (300 + 40 + 7)
• (20 + 9) = 300
• 20 + (300
• 9 + 40
• 20) +

+ (40

• 9 + 7
• 20) +7
• 9 = 6000 + (3000 + 500) + 500 + 63 + (6000 + 3000) + +(500 + 500) + 60 + 3 = 10063.

В « Книге об индийском счете» было впервые дано систематическое изложение арифметики, основанной на индийской десятичной позиционной системе счисления.

Аль-Хорезми первым ввёл в числовой ряд новое число «ноль», что расширило теорию чисел и дало возможность перейти к отрицательным числам. Перевод этого труда на латынь был выполнен в XII веке и хранится сегодня в Кембридже. Арабский текст был утерян.

В латинской транскрипции имя автора — Аль-Хорезми — звучало как «Алгоризми». Поскольку сочинение об арифметике было очень популярно в Европе, это слово стало нарицательным – средневековые европейские математики так называли арифметику, основанную на десятичной позиционной системе счисления. Позднее термин «алгоритм» стал использоваться как общее название любой системы вычислений, выполняемых по строго определённым правилам.

Так имя Мухаммеда Аль-Хорезми перешло в Алгоритми, откуда и появилось слово алгоритм.

«Краткая книга об исчислении ал-джабры и ал-мукабалы»

Около 830 г. Мухаммад ибн Муса Аль-Хорезми составил первый известный арабский трактат по алгебре, заложив, таким образом, основы математической традиции в арабском мире, существовавшей на протяжении столетий.

Алгебраическая работа называется «Китаб ал–джабр ал–мукабала», что означает «Книга о восстановлении и противопоставлении». Это наиболее известная и значительная из всех работ Аль-Хорезми. Общепризнанно, что данный трактат Аль-Хорезми является первым серьезным научным исследованием в данной области знаний.

Причина, по которой он обратился к этой теме, была проста — он планировал учить: «Наиболее легкая и полезная вещь в арифметике, например, то, что постоянно требуется человеку в делах наследования, получения наследства, раздела имущества, судебных разбирательствах, торговых отношениях или при измерении земельных участков, рытье каналов, геометрических вычислениях, а также в других случаях».

Задумывавшаяся как начальное руководство по практической математике, «Краткая книга об исчислении ал-джабры и ал-мукабалы» в первой своей части начинается с рассмотрения уравнений первой и второй степени и далее в двух заключительных разделах переходит к практическому применению алгебры в вопросах мероопределения и наследования.

Книга начинается с введения натуральных чисел, далее идет представление главной темы первого раздела книги — решения уравнений. Все представленные уравнения являются линейными или квадратными и состоят из чисел, их квадратов и корней.

числа особого вида – неизвестная величина, ее квадрат и свободный член уравнения.

Неизвестную величину Аль Хорезми называет термином «корень» (джизр) и дает следующее определение:

«Корень – это всякая вещь, умножаемая на себя, будь то число, равное или большее единицы, или дробь, меньшая ее».

Такое определение связано с тем, что при решении уравнений всегда искали не только x, но и x . Поэтому неизвестная рассматривалась как корень из квадрата неизвестной. В определении подчеркивается также, что неизвестная может принимать как целые, так и дробные значения. Термин «корень», применяемый Аль Хорезми, является, по всей вероятности, переводом санскритского слова «Мула» (корень растения), которым обозначали неизвестную в уравнении индийские математики. Позднее в арабской литературе для той же цели применяли термин «вещь» (шай).

Квадрат неизвестной назван словом «имущество» (мал) и определяется как «то, что получается из корня при его умножении на себя». Свободный член уравнения – «простое число» – Аль Хорезми называет «дирхемом»,

т. е. денежной единицей.

Что же означают слова «ал-джабра» и «ал-мукабала»? Ответ на этот вопрос один персидский математик изложил в следующих стихах:

Ал-джабра	Ал-мукабала
При решении уравненья Если в части одной, Безразлично какой, Встретится член отрицательный, Мы к обеим частям, С этим членом сличив, Равный член придадим, Только с знаком другим,- И найдём результат нам желательный.	Дальше смотрим в уравненье, Можно ль сделать приведенье, Если члены в нём подобны, Сопоставить их удобно, Вычтя равный член из них, К одному приводим их.

Таким образом, название «ал-джабра» носила операция переноса отрицательных членов из одной части уравнения в другую, но уже с положительным знаком. По-русски это слово означает «восполнение».

Поэтому в Испании, которая долгое время была под арабским владычеством, слово «алгебраист» означало совсем не математика, а костоправа. И когда Дон-Кихот был ранен в одном из поединков, его верный оруженосец Санчо Панса привёл из соседнего городка именно алгебраиста.

Слово «Аль-джебр» со временем превратилось в хорошо знакомое слово алгебра.

А слово «ал-мукабала» означало приведение подобных членов. В отличие от слова «ал-джабра», которое в форме «алгебра» стало одним из самых употребительных в математике, про «ал-мукабалу» помнят только историки науки.

Итак, при решении уравнения 6х–13=2х–5, когда мы заменяем его на 6х+5=2х+13, то делаем операцию «ал-джабра». А когда после этого заменяем члены 6х и 2х на 4х слева, а 13 и 5 на 8 справа и получаем уравнение

4х = 8, то делаем «ал-мукабалу».

Операция последующего деления обеих частей уравнения на 4 особого названия не получила.

Таким образом, действия «ал-джабр» и «ал-мукабала» заменяли применяющийся ныне перенос членов из одной части уравнения в другую с приведением подобных слагаемых.

Далее Аль-Хорезми показывает, как необходимо решать шесть стандартных видов уравнений с применением алгебраических методов решения и геометрических доказательств.

Две операции позволили Аль — Хорезми приводить всякое алгебраическое уравнение первой и второй степени к каноническим формам, которых у Аль-Хорезми шесть.

Форма уравнения	Вид уравнения	Пример
«корни равны числу»	вx = c	4x = 20
«квадраты равны числу»	ax= с	5x = 80
«квадраты равны корням»	ax = bx	5x = 10x
«квадраты и корни равны числу»	ax+ bx = c	x + 10x = 39
«квадраты и числа равны корням»	ax+ c= bx	x + 21 = 10x
«корни и числа равны квадратам»	bx + c = ax	3x + 4 = x

Все эти уравнения записывались им словесно. Интересно отметить, что во всех книгах Аль-Хорезми математические вычисления фиксируются исключительно при помощи слов, ни один символ им не использовался.

Для Аль-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Кроме того, требовалось, чтобы коэффициент при старшем члене был равен единице.

Автор излагает способы решения указанных уравнений, пользуясь приёмами ал-джабр и ал-мукабала.

Ни он, ни другие математики, писавшие по-арабски, не употребляли никаких сокращенных обозначений. В них не было нужды, ибо арабское письмо очень кратко: гласные не обозначаются, согласные и полугласные буквы просты по начертанию и сливаются по нескольку в один знак. Для написания многих слов требуется не больше времени, чем для написания некоторых наших букв (например, ж, щ).

Зато арабская грамота намного трудней нашей.

Они не признавали и отрицательных чисел: учение об отрицательных числах, знакомое им из индийских источников, они считали плохо обоснованными. Это было справедливо, но зато индийские ученые могли ограничиться одним случаем полного квадратного уравнения, тогда как Аль-Хорезми и его преемники должны были различать три случая.

Метод Аль-Хорезми — почти алгебраический

Аль-Хорезми был первым учёным, отделившим алгебру от арифметики и рассматривавшим её как отдельную ветвь математики.

Впервые в истории математики в трактате Аль-Хорезми появились общие правила решения квадратных уравнений.

И это колоссальный шаг вперед по сравнению с геометрической алгеброй греков; от него остается один шаг (правда, длиной в добрых семь с половиной веков) к алгебре символической.

Если большинство греков не видело необходимости в приложении научных знаний к практическим потребностям, то главным желанием Аль-Хорезми было поставить науку на службу человечеству, приспособить ее к практическим целям.

Содержание второй части книги составляют задачи на раздел имущества. Эта часть называется «Книга о завещаниях». В своё время она служила практическим руководством для юристов, занимавшихся разделом наследства.

Аль-Хорезми был автором значительной работы в области географии, где он дал определение широты и долготы 2402 населенных пунктов мира в качестве основы карты мира. Написал он также ряд других менее известных работ по таким темам, как астролябия, летоисчисление и солнечные часы.

Аль – Хорезми даёт правила вычисления площади квадрата, треугольника и ромба. Правила вычисления объёма, усечённой квадратной пирамиды. Им была составлена политическая история, в которой были представлены гороскопы известных деятелей.

Но, несмотря на его разносторонний круг научных интересов, главная наука его жизни – математика.

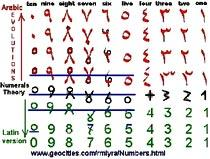
О записи числа

Используя примечания абаки, Ал-Хваризми развивал систему рукописного десятичного числа.

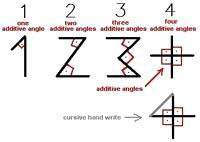
Основанный на углах, он определил номер 1, 2, 3 и 4.

Арабские 1-2-3-4 числа форматируют на наличии углов:

Номер один (1) имеет один угол.

Номер два (2) имеет два угла.

Номер три (3) имеет три угла.

Номер четыре (4) имеет четыре совокупных угла.

Номер четыре закрыт из-за рукописной руки, пишут.

И используя его знание о примечаниях рукописи абаки, он определил номер 5, 6, 7, 8, 9, 0.

Круг — символ закрытой руки, которая имеет пять пальцев.

Номер пять записан под линией.

Номер десять (2-ая рука) записан над линий.

Теоретически, круг над линей приобретает двойную ценность (десять ценностей).

Фигура абаки и рукописные круги:

• круги — символы: пять, шесть и семь были помещены ниже пишущейся линии.

• круги -символы : десять, девять и восемь были помещены выше пишущейся линии

• к кругу пять добавлен штрих с одним совокупным углом, получается номер шесть.

• к кругу пять были добавлены два штриха, с двумя совокупными углами, делающими номер семь

• к кругу десять был добавлен штрих вниз с одним углом, получается девять.

• к кругу десять были добавлены два штриха вниз, с двумя углами, уменьшающие до номера восемь.

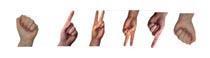
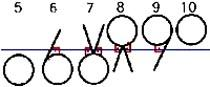
Эволюция записи чисел:

ЗАКЛЮЧЕНИЕ

Скорее всего, его научные заслуги этим не ограничиваются – однако и того, что нам известно о его трудах, дает более чем достаточно оснований считать Аль-Хорезми одним из величайших ученых Средневековья, достойного того, чтобы о нём говорили на уроках математики и в наше время.

Международный симпозиум

памятник.

международная премия «Аль-Хорезми»

Статус премии:

премия присуждается в знак признания достижений исследователей, инноваторов и изобретателей со всего мира и их вклада в различные области науки и техники, такие как инженерия, фундаментальные науки, гуманитарные науки, сельское хозяйство, биотехнологии, нанотехнологии.

Неудивительно, что известный историк науки Дж. Сартон назвал Аль-Хорезми величайшим математиком своего времени и, если принять во внимание все обстоятельства, одним из величайших всех времен.

Литература

[Электронный ресурс]//URL: https://litfac.ru/referat/jizn-i-tvorchestvo-al-horezmi/

1. Энциклопедический словарь юного математика. Составитель А.П. Савин. – М.: Педагогика, 1985

2. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989

3. Белл Э.Т. Творцы математики: Предшественники современной математики. – М.: Просвещение, 1979

4. История математики в школе: IV –VI кл. – М.: Просвещение, 1981

5 . История математики в школе: VII –VIII кл. – М.: Просвещение, 1982

6. Интернет ресурсы: http://www.myshared.ru/slide/217117/

15