«История развития учения о правильных многогранниках»

метки: Рассказ, Многогранник, Горпищенко, Правильный, Додекаэдр, Школа, Изучение, Вписываться

История развития учения о правильных многогранниках

Многогранник

1. многогранник выпуклый;

2. грани — равные друг другу правильные многоугольники;

3. в каждой вершине сходится одинаковое число рёбер;

4. все двугранные углы равны.

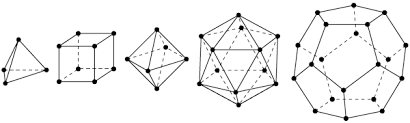
Рис. 1. Правильные многогранники

История многогранников уходит в глубокую древность и связана с именами таких учёных как Пифагор, Евклид, Архимед, Платон и Кеплер . Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Пифагор и его ученики занимались изучением правильных многогранников. Их поражала красота, совершенство, гармония этих фигур [12,с.171].

Они полагали, что материя состоит из четырёх основных элементов: огня, земли, воздуха, воды. И каждому элементу придавалась соответствующая форма.

Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий учёный, философ – идеалист Платон.

Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды. Существование пяти правильных многогранников они относили к строению материи и Вселенной. Согласно этому мнению, атомы основных элементов должны иметь форму различных Платоновых тел (рис.4).

земля

вселенная

Рис. 4. Соотнесение элементов материи и Платоновых тел

Объяснение этих ассоциаций дается таким образом:

Основные средства композиции

... элементов их формы, т. е. их соразмерность и соподчиненность. Средствами приведения первичных свойств формы к композиционному единству являются пропорции, масштабность, ритм, контраст и нюанс. Применение этих средств композиции ... спектральным составом отражаемого или излучаемого ими света. Цвет обладает такими основными характеристиками, как цветовой тон (различные оттенки цвета), насыщенность ( ...

• жар огня ощущается чётко и остро (как маленькие тетраэдры );

• воздух состоит из октаэдров : его мельчайшие компоненты настолько гладкие, что их с трудом можно почувствовать;

• вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков (самая обтекаемая форма у икосаэдров );

• в противоположность воде, совершенно непохожие на шар гексаэдры составляют землю, куб ассоциируется с устойчивостью и проводится аналогия тому, что земля рассыпается в руках, а не течет плавно, как вода.

В наше время эту систему можно сравнить с четырьмя состояниями вещества – твердым, жидким, газообразным и плазменным.

• пятый многогранник — додекаэдр — воплощал в себе «все сущее», символизировал весь мир и почитался главнейшим. Относительно додекаэдра , Платон сделал смутное замечание: «…его бог определил для Вселенной, имеющей форму сферы, и прибегнул к нему в качестве образца» [44].

Именно эти исторические предпосылки дают повод ученым называть пять правильных многогранников « Платоновыми телами».

В своем бессмертном трактате «Начала» Евклид доказал, что других правильных многогранников не существует, но греки знали об этом задолго до него. дал математическое описание многогранников в XIII Начал [21, с.105]. Предложения этой [21, с.120-131] описывают тетраэдра, октаэдра, , икосаэдра и додекаэдра в порядке. Для многогранника Евклид отношение диаметра сферы к длине .

Рис.5. (365 — 300 до н.э.) – древнегреческий , автор первого из до нас теоретического трактата «» [35, с .112].

за Евклидом изучением многогранников занимался . Убедившись в том, что нельзя шестой , Архимед стал многогранники, у которых являются правильные, но не многоугольники. 13 полуправильных многогранников, которых приписывается .

Рис.6. Архимед ( 287 . — 212 до н. э.) — математик, физик и из Сиракуз. Сделал открытий в геометрии. основы , гидростатики, автор важных изобретений [35, с. 29].

Правильные многогранники

... правильные многогранники в системе гармоничного устройства мира И. Кеплера. Все та же вера в ... В сферу орбиты Сатурна он вписывает куб, в куб - сферу Юпитера, в сферу Юпитера - тетраэдр, и так далее последовательно вписываются друг в друга сфера Марса - додекаэдр, сфера Земли - икосаэдр, сфера Венеры - октаэдр, сфера ... созданные искусством человека формы". Создания природы, приведенные в этой ...

Но 5-ти Платоновых тел было еще раз на небосводе естествознания.

к Европе XVI – XVII вв., жил и творил замечательный астроном, Иоганн Кеплер.

.7 Иоганн Кеплер немецкий математик, , , оптик, законов движения Солнечной системы [15, 19].

Представим себя на Кеплера. ним различные таблицы – цифр. Это результаты движения планет системы – как его , так и великих предшественников – . В этом мире работы он хочет некоторые . Иоганн Кеплер, для правильные многогранники любимым предметом , предположил, что связь между правильными многогранниками и открытыми к тому планетами системы. Согласно предположению, в сферу Сатурна можно куб, в который сфера орбиты . В неё, в свою очередь, тетраэдр, описанный сферы Марса. В сферу Марса вписывается , в который вписывается орбиты . А она описана около , в который вписана орбиты Венеры. этой описана около , в который вписывается Меркурия. Такая Солнечной (рис. 8) получила «Космического кубка» .

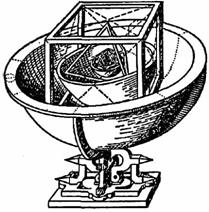
Рис 8. Космический кубок .

Результаты вычислений учёный в книге «Тайна ». Он считал, что тайна раскрыта. Год за учёный уточнял наблюдения, перепроверял коллег, но, наконец, в себе отказаться от заманчивой . Однако её следы в третьем законе , где говориться о средних расстояний от .

Сегодня можно с утверждать, что расстояния планетами и их никак не связаны с . Конечно, структура системы не является , но истинные , по которым она устроена так, а не , до сих пор не известны. Идеи оказались ошибочными, но без , иногда неожиданных, не может наука.

Кроме многогранников, из правильных – Платоновых тел получить так называемые звездчатые многогранники. Их четыре. Первые два открыты И. (1571 – 1630 гг.), а два были построены двести лет спустя математиком и Луи Пуансо (1777 – гг.).

Именно поэтому звездчатые многогранники название тел – Пуансо. [15 с. 20-25].

Идеи и Кеплера о связи многогранников с гармоничным мира и в время нашли продолжение в интересной гипотезе, которую в 80-х гг. московские инженеры Н. , В. Макаров и В. Морозов [14, с.

Они считают, что ядро имеет и свойства растущего , оказывающего воздействие на всех природных , идущих на .

Многогранники в архитектуре

... трехгранного угла. Аналогично определяется понятие многогранного угла (рис. 3). 3. Многогранник В стереометрии изучаются фигуры в пространстве, называемые телами. Наглядно (геометрическое) тело надо представлять себе ... будет дано позже. 4. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и ...

Рис.9. Слева : Морозов-Гончаров-Макаров.

Лучи кристалла, а точнее, его поле, икосаэдро-додекаэдровую структуру (рис.10).

Она проявляется в том, что в коре как бы проступают вписанных в шар правильных многогранников: и додекаэдра.

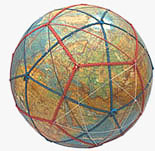
Рис 10. Икосаэдро-додекаэдровая Земли.

Многие полезных тянутся вдоль сетки; 62 вершины и рёбер многогранников, авторами , обладают рядом свойств, позволяющих некоторые непонятные . Если на глобус очаги крупных и примечательных и цивилизаций Древнего , можно закономерность в их расположении географических полюсов и планеты. Многие полезных тянутся вдоль сетки. Еще более вещи происходят в пересечения ребер. Здесь очаги древнейших и цивилизаций: Перу, Монголия, , Обская культура и . В этих точках максимумы и минимумы давления, завихрения Мирового . В этих узлах озеро Лох-Несс, треугольник. исследования Земли, , определят отношение к научной гипотезе, в , как видно, многогранники занимают место. Итак, изучали учёные , средних , и их идеи оказались современными – это были попытки систематизации нас мира. предвидение Пифагора о том, что откроет человечеству к тайне Мироздания, , хотя пришлось более 2-х .

Литература

[Электронный ресурс]//URL: https://litfac.ru/referat/rasskaz-o-gorpischenko/

1. Александров А.Д. Выпуклые многогранники, М.—Л., Гостехиздат, 1950.

2. Александров А.Д. Геометрия для 10-11 классов: Учеб. Пособие для учащихся школ и классов с углубленным изучением. математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. — М.: Просвещение, 1992.

3. Александров А.Д. Что такое многогранник? // Математика в школе. – 1981 ,

1, 2.

4. Атанасян Л.С. Геометрия: Учеб. для 10-11 кл. общеобразовательных учреждений. / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. — М.: Просвещение, 2006.

5. Ашкинузе В. Г. Многоугольники и многогранники. Энциклопедия элементарной математики, кн. IV (Геометрия), М:Физматгиз, 1963..

6. Белим С.Н., Белим С.В. Конструктор оригами. Многогранники. Омск – 2003.

7. Белим С.Н., Белим С.В. Правильные многоугольники в оригами. Омск – 2003.

8. Болтянский В.Г. Выпуклые многоугольники и многогранники. / В.Г. Болтянский, И.М. Яглом // Математика в школе. — 1966, № 3.

   13 стр., 6322 слов

   Геометрия и искусство

   ... часть развивает активно-действенный подход к реализации эстетического потенциала геометрии в процессе обучения (В.Г. Болтянский, Н.В. Гусева, О.А. Кобалия, Н.Л.Рощина, Н.И.Фирстова). Основой, позволившей рассмотреть ... А.Пуанкаре и др.) и специалисты в области математического образования (В.Г. Болтянский, В.А. Крутецкий и др.), видение красоты геометрии определяет не только эстетико-ценностную ...

9. Болтянский В.Г. Элементарная геометрия: Кн. для учителя. / В.Г. Болтянский. — М.: Просвещение, 1985..

10. Веннинджер М. Модели многогранников. — М. : Мир, 1974.

11. Глаголев Н.А. Геометрия: Стереометрия. / Н.А. Глаголев, А.А. Глаголев. — М.: Учпедгиз, 1958.

12. Глейзер Г.И. История математики в школе IX–X классы – М.: Просвещение, 1983.